Прогнозирование, основанное на использовании моделей временных рядов

Поскольку tm = 2,07 и это значение больше t-критериев для каждого из коэффициентов, то делаем вывод об их статистической значимости.

Определим интервалы доверия для параметров регрессии [ЕЛИ, с. 57].

Для расчета доверительного интервала определяем предельную погрешность для каждого коэффициента:

Δa = tтаб.ma = 2,0690 · 0,0017 = 0,0034,

Δb = tтаб.mb = 2,0690 · 1,3167 = 2,7242,

Следовательно, экстремальные значения для каждого коэффициента следующие:

min a = a - Δa = 0,0220 - 0,0034 = 0,0186, max a = a + Δa = 0,0220 + 0,0034 = 0,0254,

min b = b - Δb = 4,8705 - 2,7242 = 2,1463, max b = b + Δb = 4,8705 + 2,7242 = 7,5947.

Таким образом, доверительные интервалы для коэффициентов регрессии следующие:

a Î (0,0186; 0,0254),

b Î (2,1463; 7,5947).

Изобразим диаграмму рассеяния и прямую регрессии.

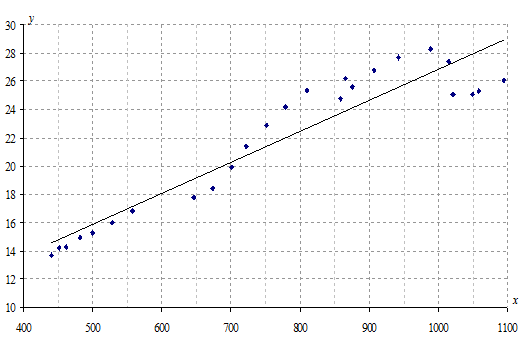
б) Постройте линейный временной тренд для функции спроса.

Идентифицируем переменные: t - независимая временная переменная (фактор), y - зависимая переменная (показатель). Пусть модель специфицирована в линейной форме:

y = at + b + u,

где a, b - параметры модели, u - стохастическая составляющая (остатки).

Используем метод наименьших квадратов [ЛЕЩ, с.29].Запишем систему нормальных уравнений, используя в качестве неизвестную переменную - переменную t:

Расчет параметров значительно упрощается, если за начало счета времени (t = 0) принять центральный интервал (момент).

При нечетном числе уровней (например, 25), значения t = 0 - условного обозначения времени будет отвечать среднему 1971 году: